DeepMind’s AlphaGeometry2 has made headlines by outperforming the average International Mathematical Olympiad (IMO) gold medalist in solving Euclidean geometry problems. AlphaGeometry2 is a significant upgrade to AlphaGeometry that addresses previous limitations and enhances performance in several key areas. These improvements have resulted in a substantial leap in performance, with AG2 achieving an 84% solve rate from 2000-2024 IMO geometry problems
For a mathematician, this is both an exciting development and a moment for critical reflection—what does it mean for AI to excel at problems traditionally reserved for human ingenuity?
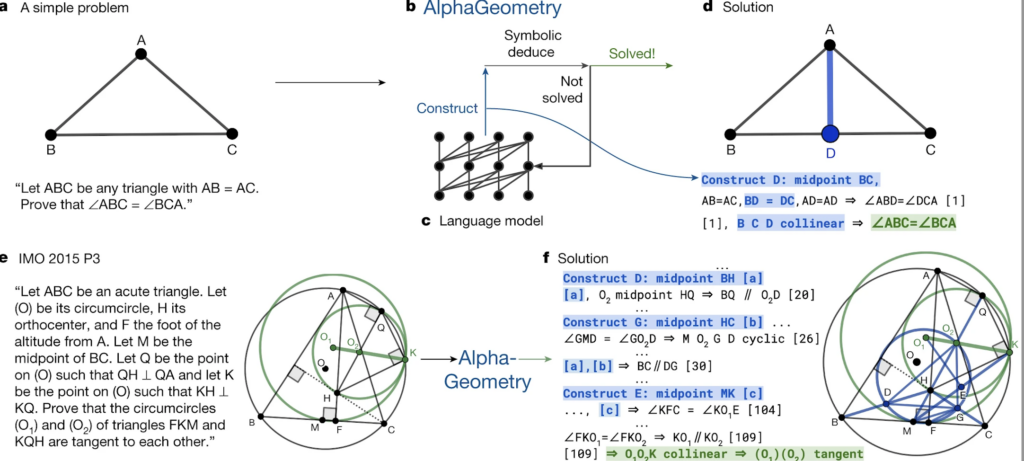
At its core, AlphaGeometry2 employs a hybrid approach, merging the symbolic precision of classical mathematics with the statistical learning power of neural networks. It utilizes Google’s Gemini AI model to suggest constructive steps in a proof while relying on a symbolic engine to ensure logical consistency. The model has been trained on a staggering 300 million synthetic theorems and proofs, allowing it to build intuition (in a computational sense) about geometry problems from past IMO competitions.

The results are impressive: AlphaGeometry2 successfully solved 42 out of 50 past IMO problems, surpassing the average gold medalist score of 40.9. However, it fell short when confronted with a more difficult, unpublished set of 29 geometry problems, managing only 20 correct solutions. This limitation hints at a crucial mathematical challenge—how well can AI generalize beyond its training set?
The significance of this development extends beyond competition math. Proving theorems requires both rigorous deduction and creative intuition—skills that are foundational to mathematical discovery. While AlphaGeometry2 operates within a predefined set of logical rules, it also introduces new constructions to solve problems, mimicking the problem-solving behavior of a human mathematician. This suggests that AI could one day assist in formalizing proofs or even discovering new mathematical results.
Of course, AlphaGeometry2 isn’t perfect. It struggles with nonlinear equations, inequalities, and problems involving a variable number of points. Furthermore, while its hybrid approach merges symbol manipulation with neural networks, the philosophical debate rages on—should AI reasoning be built on rigid symbolic logic, or should it rely on massive amounts of data to approximate solutions? The contrast between symbolic reasoning and neural networks remains a defining question in AI and mathematics.
For mathematicians, AlphaGeometry2 presents both an opportunity and a challenge. It reinforces the idea that AI can be a powerful assistant in tackling difficult mathematical problems, yet it also underscores the limitations of machine reasoning. While DeepMind’s model is remarkable, it is still far from replicating the creative leaps of human mathematicians.
The final takeaway? AI can certainly solve IMO problems, but can it create mathematics? That, for now, remains a uniquely human pursuit.
For more details, check out the full research papers here:
• DeepMind’s AlphaGeometry2 Research Paper (arXiv)
• Solving Olympiad Geometry Without Human Demonstrations (Nature)
Note: Edited with QGenAI.


Comments